CollDet - A Library for Collision Detection
CollDet is a fast, robust, and accurate library for collision detection
between 3D objects undergoing rigid motion. It is designed to be used in
interactive 3D realtime-applications. CollDet is based on the portable
open source scenegraph OpenSG.
Collision Detection Pipeline
The collision detection process can be regarded as a pipeline of successive filters.
The front-end of the pipeline consists mainly of a queue which stores objects.
During run-time, objects, together with their current position, are entered in the queue
when they have been moved.
The collision interest matrix filters out all objects pairs of no intersect. After that,
object pairs are filtered further by two neighborfinding stages and finally by an exact
collision test.
(For more details on that, we refer the interested user to the paper
Optimizing the Collision Detection Pipeline).
Slides
I presented the library at the Siggraph 07 BoF.
Here are the
slides.
Features
- Boxtree and Dop-Tree for the narrow-phase
- Grid for accelerating the broad-phase
- Convex hull pre-checks (not based on i_collide)
- Supports polygon soups
- The whole pipeline is implemented
- You can define your own collision callback classes
- Support for multi-threading
- Easy-to-use interface
- Runs on Linux, Mac, and Windows
Prerequisites
- OpenSG Version 1.2 or higher
- gcc 3.5 or higher, Visual Studio 2003 or higher, or Intel compiler 8.0
Download
You can download the source code
of CollDet here.
Here is the documentation (generated
using doxygen)
as individual HTML pages,
as a PDF,
and as a ZIP archive.
Note that there is a
copyright / license
that basically says: you can use it for free for academic purposes, but
if you want to use it for commercial or other non-academic purposes, then
we must negotiate some royalty (which could be a hardware donation, money, etc.).
If you are interested, please send me an
email.
Benchmarking Results
The diagrams show the performance of our library ("bx" marks the Boxtree and "do" the DopTree) compared to other collision detection libraries, namely, V-Collide ("vc"), PQP, OPCODE ("op"), and FreeSOLID ("so"). For further information about our Benchmarking Suite, including a description of the benchmarking procedure, and much more diagrams, please visit our project homepage.
Publications
- The BoxTree: Exact and Fast Collision Detection of Arbitrary Polyhedra, SIVE95 (First Workshop on Simulation and Interaction in Virtual Environments), University of Iowa, July 1995.
- Real-time and Exact Collision Detection for Interactive Virtual Prototyping, Proc. of the 1997 ASME Design Engineering Technical Conferences, September 14-17, 1997, Sacramento, California. Paper # CIE-4306.
- Rapid Collision Detection by Dynamically Aligned DOP-Trees, Proc. of IEEE Virtual Reality Annual International Symposium; VRAIS '98. Atlanta, Georgia; March 1998. Pages 90-97.
- Optimizing the Collision Detection Pipeline, Proc. of the First International Game Technology Conference (GTEC), Hong Kong, 18-21 January 2001.
- A Benchmarking Suite for Static Collision Detection Algorithms, International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision (WSCG), January 29 - February 1, 2007.
For further information please visit also our project homepage.
- More publications can be found on our
list of publications.
Screenshots
Click on the pictures to enlarge.
Intersection
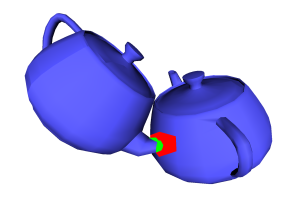 |
On the left side you can see the intersecting triangles. Click on the image to see a small video. |
Doptree
 |
Discrete orientation polytopes (DOPs) are convex polytopes whose faces can have only
normals which come from a fixed small set of orientations (k-DOPs). In order to be able to apply an interval
test to DOPs, one restrict the set of orientations further such that for each orientation of the set
there is also an anti-parallel one. Thus, this special kind of k-DOPs can be viewed as a generalization of
axis-aligned boxes. We have determined 24 as the optimal number of orientation.
(For further information: Rapid Collision Detection by Dynamically Aligned DOP-Trees)
The animation on the right shows the first 10 DOP-Tree levels.
|
Boxtree
 |
These axis-aligned bounding volumes are called Box Tree. Of course,
when objects move, they are no longer aligned with respect to the world s coordinate frame.
So, when using this type of BVs, the task is to devise algorithms for efficient
overlap tests of tumbled bounding boxes.
Octrees are a special case of BoxTrees. However, BoxTrees allow for finer control on the balancedness.
Each node in the BoxTree stores only: the name a of the splitting axis, two positions, two pointers
(to the left and right sub-box), and, for leaves only, a pointer to the polygon(s)
associated to the leaf.
(For further information:
Virtual Reality in Assembly Simulation - Collision Detection, Simulation Algorithms, and Interaction Techniques )
The animation on the right shows some level of the boxtree. |
Robustness
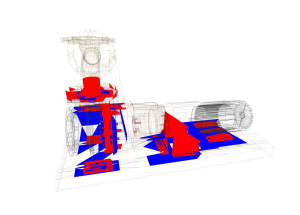 |
Some scenarios for collision detection algorithms include very specific
configurations. For example, data gathered from CAD programs contain numerous intersections between coplanar triangles.
Therefore, the robustness of the triangle intersection test, but also the numerical stability of the bounding volume tests
play an important role for a proper collision response.
|
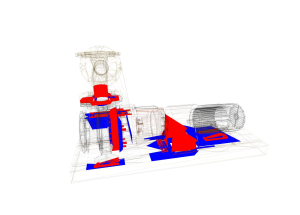 |
The pictures on the left side shows a snapshot from a CAD generated scene. The upper left picture shows the intersecting triangles
found by CollDet, the lower left picture those triangles found by another collision detection library. As you can see, CollDet finds 50% more intersecting
triangle pairs than the other library. Tests have shown, that many other libraries miss most of the intersecting coplanar triangles.
Click here to see a video of the complete scene. |
Separating Planes
 |
The separating plane algorithm just needs the set of vertices of the convex hull
and its adjacency map. It is based on the following notion: Two objects do not intersect iff there
is a plane such that all vertices of the objectes are on different sides. Such a plane is called
separating plane
The animation on the right shows the line between the closest vertices.
|
|